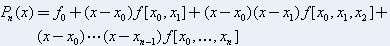 kde výraz
kde výraz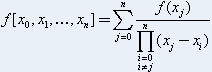 se nazývá poměrná diference řádu n. Pro lepší pochopení :
se nazývá poměrná diference řádu n. Pro lepší pochopení :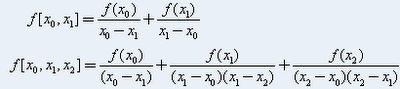 V praxi se využívá následujícího schématu:
V praxi se využívá následujícího schématu:Pro konstrukci polynomu se využijí čísla na horní diagonále ve výše uvedeném schématu.
Příklad: Uvažujme funkci y=f(x) zadanou následující tabulkou:
 Pak pro výpočet koeficientů platí:
Pak pro výpočet koeficientů platí: A tedy Newtonův interpolační polynom je tvaru:
A tedy Newtonův interpolační polynom je tvaru: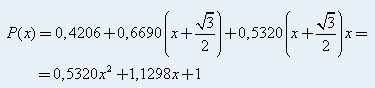 Na závěr porovnání, jak interpolační polynom axproximuje zadanou funkci:
Na závěr porovnání, jak interpolační polynom axproximuje zadanou funkci: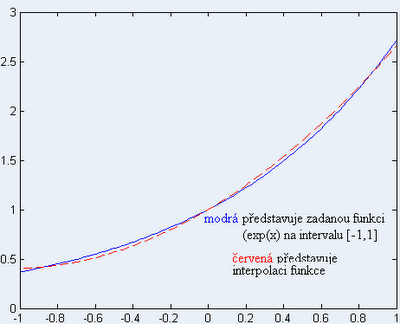




Žádné komentáře:
Okomentovat