Zajímavosti z teorie čísel 2
V předchozím příspěvku bylo dokázáno, že množina všech prvočísel je nekonečná, tedy za každým přirozeným číslem leží nekonečně mnoho prvočísel. Vyvstává další otázka, jak jsou prvočísla v rámci množiny přirozených čísel uspořádána.
Na tuto otázka nalezl odpověď američan polského původu Stanislaw Marcin Ulam (1909-1984).
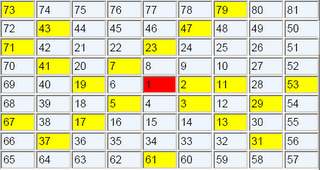Ulam při jednom ze svých pokusů začal do polí nekonečné šachovnice zapisovat do spirály přirozená čísla. Posléze si všiml, že prvočísla tvoří jakési uhlopříčky. Tedy rozmístění prvočísel se řídí nějakou zákonitostí. Tato zákonitost ovšem nebyla zatím přesně popsána.Předchozí díl: Důkaz nekonečnosti prvočísel.
Žádné komentáře:
Okomentovat