Zajímavosti z teorie čísel 5
Dosti důležitou úlohou v rámci i mimo teorii čísel je určení, zda dané přirozené číslo n je prvočíslem. Nejznámnější metodou je prvočíselný rozklad, kdy dělíme dané číslo postupně všemi prvočísly, která jsou menší nebo rovna než √n.Pro malá čísla, řekněme desetimístná je tato metoda docela vhodná, na počítači probíhá velmi rychle. Ale pokud bude mít dané číslo padesát míst, pak by musel i velmi rychlý počítač pracovat několik miliard let.Poněkud lepší metodou je využití upravené malé Fermatova věty:
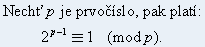Tedy spočítáme 2p-1 a určíme jeho zbytek po dělení číslem p. Jestliže vyjde zbytek různý od 1, pak je jisté, že číslo p není prvočíslo, ale je číslo složené. Ale i když zjistíme že zbytek je roven 1, i pak nemusí být dané číslo prvočíslem (např. 341) .Malá Ferm. věta je pouze nutnou, nikoliv postačující podmínkou pro prvočíselnost. Řešení tohoto problému našli v roce 1986 matematici Adleman, Rumely, Cohen, Lenstra a Pomerance - ARCLP test provočíselnosti. Na superpočítačích trvá tento test pro 20místné číslo asi 10 sekund a pro 50místné číslo asi 15 sekund.
Existují i další metody zjišťování prvočíselnosti, které ovšem pracují pouze pro čísla v určitém speciálním tvaru.
Žádné komentáře:
Okomentovat